Measuring the Drag Difference Between Two Hulls
People often ask, “I have a swimming pool, how can I see if one boat has more drag than another? Well it is quite easy, or at least the theory is. A bar is fixed between the two boats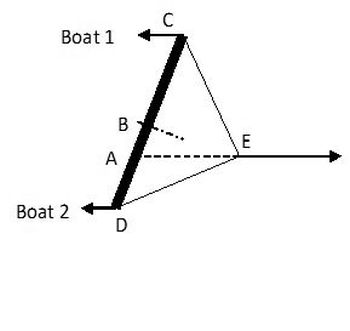 
with a length between the two fixing points C and D equal to L (the solid line in the diagram) and the boats towed. The one with the least drag will pull ahead. Point B is central between the two towing points. You sight along the towline and project it to the bar at point A.
The % difference in drag between the two boats is:
=100* 2*AB/(L/2-AB)
For IOMs a 2m bar (a mast section is ideal) is a good length. To make it easy to estimate the distance AB a series of tape wraps can be used so the bar looks like a dashed line:
The length of the strops (CE and DE) is not critical but a good starting point is to make each side about 1400mm. Each side must be exactly the same length.Long strops will aid stability but make projection to get point A more difficult.
If there is 2m between the connection points then each centimetre distance of AB closely approximates a 2% difference in drag.
The practical difficulties are that firstly the radio power needs to be on to keep the rudders straight, secondly it can take some time for the whole thing to settle down so everything needs to be straight before you start, and it may take a few runs to get the method going. Also the connection of the bar to the boats needs to be such that the boats cannot change the distance they are apart.
The other thing that must be kept in mind is that a 2% difference in drag does not translate to 2% difference in speed. The results will vary slightly but for IOMs at 1.5 knots a 2% drop in drag will result in about a 1% increase in speed while at 2.5 knots a 2% drop in drag will only result in about a 0.5% gain in speed.
Happy testing ©Colin Thorne March 2013
Gadgets